问题
计算题
如图，水平轨道AB与半径为R="1.0" m的竖直半圆形光滑轨道BC相切于B点．可视为质点的a、b两个小滑块质量ma=2mb="2" kg，原来静止于水平轨道A处，AB长为L=3.2m，两滑块在足够大的内力作用下突然分开，已知a、b两滑块分别沿AB轨道向左右运动，va = 4.5m/s，b滑块与水平面间动摩擦因数
，g取10m/s2．则
(1)小滑块b经过圆形轨道的B点时对轨道的压力．
(2)通过计算说明小滑块b能否到达圆形轨道的最高点C．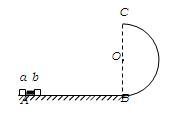
答案
⑴系统的动量守恒可得mava＝mbvb，①（2分 ）
又ma=2mb="2" kg ， va ="4.5m/s "
解得：vb ="9.0m/s " ②（1分 ）
设滑块b到达B点时的速度为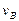
，由动能定理得，
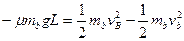③ （2分 ）
刚进入圆轨道时,设滑块b受到的支持力为FN,由牛顿第二定律得，
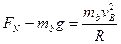④ （2分 ）
由牛顿第三定律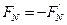
⑤（1分 ）
由③④⑤得滑块b对轨道的压力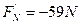
，方向竖直向下（2分 ）（没有说明方向扣1分）
⑵若小滑块b能到达圆轨道最高点,速度为vC
则由机械能守恒，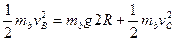
⑥（2分 ）
解得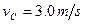
⑦ （2分 ）
小物块b恰能过最高点的速度为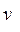
，则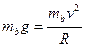
⑧（2分 ）
解得，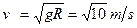
⑨（1分 ）
因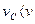
，故小滑块b不能到达圆轨道最高点C.（1分 ）