如图15所示，水平桌面上有一轻弹簧，左端固定在A点，弹簧处于自

问题计算题

如图15所示，水平桌面上有一轻弹簧，左端固定在A点，弹簧处于自然状态时其右端位于B点．水平桌面右侧有一竖直放置的光滑圆弧形轨道MNP，其半径R＝0.8 m，OM为水平半径，ON为竖直半径，P点到桌面的竖直距离也是R，∠PON＝45°第一次用质量m₁＝1.1 kg的物块(可视为质点)将弹簧缓慢压缩到C点，释放后物块停在B点(B点为弹簧原长位置)，第二次用同种材料、质量为m₂＝0.1 kg的物块将弹簧也缓慢压缩到C点释放，物块过B点后做匀减速直线运动，其位移与时间的关系为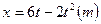，物块从桌面右边缘D点飞离桌面后，由P点沿圆轨道切线落入圆轨道．(g＝10 m/s²，不计空气阻力)

求：(1)BC间的距离；

(2)m₂由B运动到D所用时间；

(3)物块m₂运动到M点时，m₂对轨道的压力．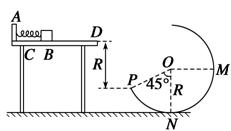

答案

(1)由x＝6t－2t²知

v_B＝6 m/s　a＝－4 m/s² (2分)

m₂在BD上运动时－m₂gμ＝m₂a

解得μ＝0.4 (1分)

设弹簧长为AC时，弹簧的弹性势能为E_p

m₁释放时E_p＝μm₁gs_BC (1分)

m₂释放时E_p＝μm₂gs_BC＋m₂v_B² (1分)

解得s_BC＝0.45 m (1分)

(2)设m₂由D点抛出时速度为v_D，落到P点的竖直速度为v_y

在竖直方向v_y²＝2gR，解得v_y＝＝4 m/s (1分)

在P点时tan 45°＝ (1分)

解得v_D＝4 m/s (1分)

m₂由B到D所用的时间t＝＝0.5 s (2分)

(3)m₂由P运动到M的过程，由机械能守恒定律得

m₂v_P²＋m₂g(R－Rcos 45°)＝m₂v_M²＋m₂gR (2分)

在M点时，对m₂受力分析，由牛顿第二定律得

F_N＝m (1分)

解得F_N＝(4－) N

由牛顿第三定律知，小球对轨道的压力为(4－) N (1分)