问题
计算题
一质量为10kg的小球，从距地面高度为H的地方沿光滑轨道滑下来，进入一半径R=5m的光滑圆形轨道内，小球在最高点时对轨道的压力为小球重量，如图所示，经过最高点后沿圆形轨道的最低点进入另一光滑半径为2R圆形轨道I，在该圆形轨道能上升的最大高度为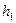
。假设第二次重复第一的运动仍从半径为R的圆形轨道的最低端进入另一光滑平直斜面轨道II，轨道足够长，能上升的最大高度为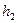
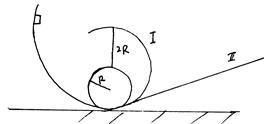
试求（1）从静止开始下滑时的最大高度H
(2)比较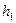、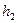与H的大小关系（
用><=表示）
答案
⑴设下落距地面的高度为H，在半径为R的圆形轨道最高点时的速度为v,在整个下落过程中机械能守恒有
mgH =mg2R+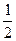
mv2 ①
在最高点做圆周运动
N+mg=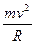
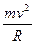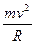2mg= ②
由①.②方程组得 H=3R
⑵
第一次从最低点进入轨道I仍满足机械能守恒，因为是圆弧在最高点时速度大小不为零
mgH =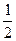mv21+mgh1 h1>H
第二次从最低点进入II轨道仍满足机械能守恒，因为平直轨道最高点时速度为零
mgh2="mgH " h2=H