问题
计算题
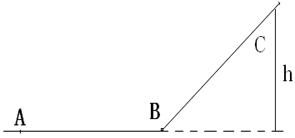
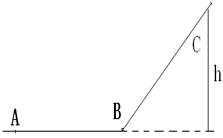
（16分）如图所示，有一粗糙水平面AB与一光滑的、很长的斜面BC在B点平滑连接，M = 2kg的物体与水平面见的动摩擦因素µ=0.4，现使其从A点以VA=8m/s的水平速度向B运动，SAB=6m物体经过B点后沿斜面上滑，之后又回滑经过B点而停在水平面上。求：
(1)物体回到B点时的速度VB.
(2)物体沿斜面上升的最大高度h
(3)物体停在水平面上的位置（用A点描述）
答案
(1)uB=4m/s (2)H=1.6m
（3）SAD=4m
(1)回到B点时速度与向右滑到B点时速度相等，在AB段用动能定律：
-µMgSAB=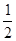
MuB2-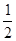MuA2 (3分)
uB=4m/s (2分)
(2)从B点到最高点机械能守恒：
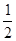MuB2=MgH (3分)
H=1.6m (2分)
（3）从B点到停止点用动能定理：
-µMgSBD=0-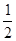MuB2 (3分)
SBD=2m (1分)
则：SAD=4m (2分)
本题考查动能定理和机械能守恒定律的应用，在由A到B得过程中，物体克服摩擦力做功等于动能的减小量，列公式求解，从B点到最高点，因为只有重力做功，机械能守恒，以水平面为零势面，列式求解