问题
选择题
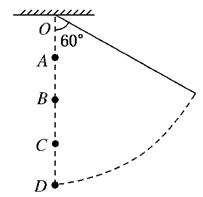
一根长为l的不可伸长的轻绳,一端系一小球,另一端悬挂于O点.将小球拉起使轻绳拉直并与竖直方向在60°角,如图所示,在O点正下方有A､B､C三点,并且有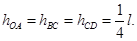
当在A处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度为hA;当在B处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度为hB;当在C处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度hC,则小球摆动的最大高度hA､hB､hC之间的关系是( )
A．hA=hB=hC
B．hA>hB>hC
C．hA>hB=hC
D．hA=hB>hC
答案
答案：D
设小球碰钉后恰好能做圆周运动的半径为R,在圆周运动的最高点处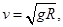
由动能定理有:
mv2-0=mgh-mgh′.
代入数据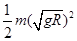
-0=mglcos60°-mg2R,
解得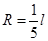
故小球绕C点能做圆周运动,绕AB两点均不能做圆周运动,由单摆运动机械能守恒可知,摆到左边的最大高度均等于原来高度hA=hB=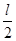
,故选D.