问题
计算题
在一次特技表演中，一电动小车的运动路径运动如图所示，小车从A点由静止出发，沿粗糙的水平直轨道运动L后，由B点进入半径为R的光滑竖直圆形轨道，运动一周后又从B点离开圆轨道进入水平光滑轨道BC段，在C与平面D间是一水池.已知小车质量m=0.1kg、L=10m、R=0.32m、h=1.25m、s=1.50m，在AB段所受阻力为0.3N.小车只在AB路段可以施加牵引力，牵引力的功率为P=1.2W，其他路段电动机关闭.问：要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台D上，小车电动机至少工作多长时间？
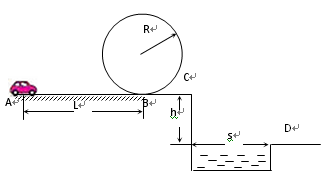
（g取10m/s2）
答案
= 
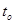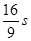
解：设车刚好越过圆轨道最高点，设最高点速度为v2，最低点速度为v1
在最高点由牛顿第二定律得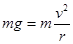 
………（1分）
由机械能守恒定律得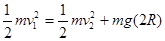 
…………（2分）
解得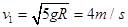 
……………………………………（1分）
小车在离开C点后做平抛运动
由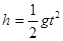
得
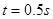……………………………………（1分）
……………………………………………………（1分）
，所以小车能够越过蓄水池………………………（1分）
设电动机工作时间为
，在AB段由动能定理得
……………………………………………（2分）
解得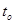= 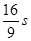……………………………………………（1分）