问题
计算题
如图所示，半径为R的半圆形光滑轨道固定在水平地面上，A、B两点在同一竖直线上，质量为m的小球以某一初速度从C运动自A点进入轨道，它经过最高点B处飞出又落回到C点，AC=2R，求小球自A点进入轨道时的速度大小.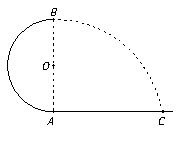
答案
解：设小球在B点速度为vB，
由平抛运动规律有2R=vB 
（2分）
得 vB="2R" 
（2分）
设小球在A点速度为vA，由机械能守恒得：
mvA2=mvB2+2mgR （2分）
所以 vA= （2分）
现根据平抛运动规律解出B点时的速度。在光滑圆轨道上只有重力做功，根据机械能守恒可得A点速度。