问题
计算题
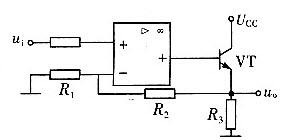
如图所示，光滑水平面MN上放两相同小物块A、B，左端挡板处有一弹射装置P，右端N处与水平传送带理想连接，传送带水平部分长度L=8m，沿逆时针方向以恒定速度v =2m/s匀速转动。物块A、B（大小不计）与传送带间的动摩擦因数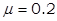
。物块A、B质量mA=mB=1kg。开始时A、B静止，A、B间压缩一轻质弹簧，贮有弹性势能Ep=16J。现解除锁定，弹开A、B，弹开后弹簧掉落，对A、B此后的运动没有影响。g=10m/s2。求：
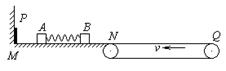
（1）物块B沿传送带向右滑动的最远距离。
（2）物块B从滑上传送带到回到水平面所用的时间。
（3）若物体B返回水平面MN后与被弹射装置P弹回的A在水平面上发生弹性正碰，且A、B碰后互换速度，则弹射装置P至少对A做多少功才能让AB碰后B能从Q端滑出。
答案
（1）
（2）
（3）8J
题目分析：（1）解除锁定后机械能守恒、动量守恒
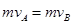
B木块向右作减速运动
（2）B木块向右作减速运动的时间
B木块向左作加速运动速度等于传送带速度时
B木块与传送带共速一起向左匀速运动
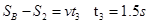
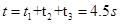
（3）B能从Q端滑出一定有
A与B质量相等，完全弹性碰撞后速度互换，则碰后A、B的速度v′A=v′B≥
W＝
mAvA’2－mAvA2≥8J。
点评：弹簧弹开的过程中，系统机械能守恒，结合动量守恒，解得A和B的速度，B滑上传送带做匀减速运动，当速度减为0时，向右运动的距离最大，由动能定理即可求解；（2）物块B先向右做匀减速运动，直到速度减小为0，然后反方向做匀加速运动，到皮带左端时速度大小仍为vB由动量定理解出运动时间，分别求出B向右匀减速运动因摩擦力而产生的热能和向左匀加速运动因摩擦力而产生的热能，进而求出总热能．