问题
计算题
如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点,一轻质弹簧左端A固定,另一端拴接一个质量为m的小球B,质量也为m的小球C靠在B球的右侧,现用外力作用在C上,使弹簧被压缩了0.4R(弹簧仍在弹性限度内)。这时小球静止于距离P端3R的水平轨道上,若撤去外力,C球运动到轨道的最高点Q后又恰好落回到原出发点。已知重力加速度为g。求
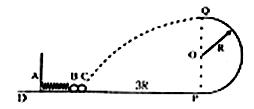
(1)小球C运动到Q点时对轨道的压力多大?
(2)撤去外力前的瞬间,弹簧的弹性势能EP是多少?
答案
(1)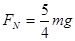 (2)
(2)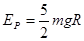
题目分析:(1)设小球经过最高点Q时的速度为v,由平抛规律有:
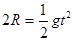
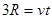
联立两式得: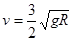
小球C在最高点,由动力学方程得: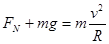
解得: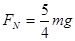
(2)设小球C离开小球B时的速度为v0,由机械能守恒有:
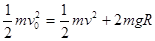
弹簧恢复到原长时脱离,则由能量守恒有: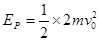
联立上述各式得: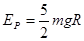
点评:撤去外力前的瞬间,弹簧的弹性势能作用下,B、C两球获得动能,因此借助平抛运动求出C球抛出速度,再由机械能守恒算出小球C被弹出的速度,从而根据能量守恒,确定撤去外力时弹簧的弹性势能..
