问题
计算题
（10分）如图所示，跨过同一高度处的光滑滑轮的细线连接着质量相同的物体A和B。A套在光滑水平杆上，定滑轮离水平杆高度为h="0.2" m。开始让连A的细线与水平杆夹角θ=53°，由静止释放，求在以后的过程中A所能获得的最大速度。
（已知cos53°=0.6，sin53°=0.8，g="10" m/s2）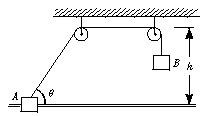
答案
1m/s
题目分析：当左侧线竖直时，A的速度最大，此时B的速度为零
此时B下降高度：hB＝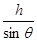
－h＝h（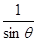
－1）＝0.2×（
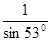－1）＝0.05m
对A、B组成的系统，由机械能守恒定律得：
mghB＝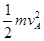
则：vA＝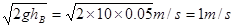
点评：本题难度中等，能够判断出当左侧线竖直时，A的速度最大是关键，以整体为研究对象，由于没有其他能量产生，因此整体系统的机械能守恒
