问题
计算题
如右图所示,光滑细圆管轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,C为半圆的最高点。有一质量为m,半径较管道略小的光滑的小球以水平初速度v0射入圆管.
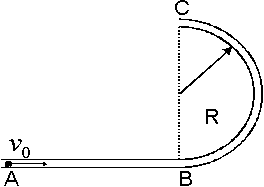
(1)若要小球从C端出来,初速度v0应满足什么条件?
(2)在小球从C端出来瞬间,对管壁压力有哪几种情况,初速度v0各应满足什么条件?
答案
（1）v0>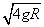
（2）有三种可能，
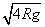＜v0＜
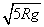.对轨道内有压力，v0=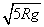正好没有压力，v0>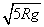对轨道外侧有压力
题目分析：(1)小球恰好能达到最高点的条件是vC=0,
由机械能守恒定律,此时需要初速度v0满足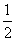
mv20=mg2R,得v0=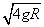,因此要使小球能从C端出来需满足入射速度v0>.
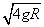(2)小球从C端出来瞬间,对管壁作用力可以有三种情况:
①刚好对管壁无作用力,此时重力恰好充当向心力,由圆周运动知识mg=m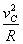
.
由机械能守恒定律,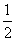mv20=mg2R+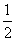mv2C, 联立解得v0=.
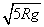②对下管壁有作用力,此时应有mg>m,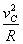
此时相应的入射速度v0应满足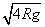＜v0＜.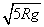
③对上管壁有作用力,此时应有mg<m,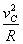
此时相应的入射速度v0应满足v0>.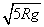
点评：本题借助机械能守恒定律求解到最高点的速度，并借助向心力知识分析对轨道压力情况。