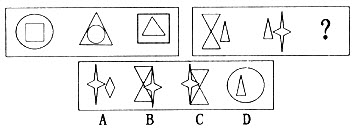
问题
计算题
如图所示，让摆球从图中的A位置由静止开始下摆，正好摆到最低点B位置时线被拉断.设摆线长ι＝1.6 m，悬点到地面的竖直高度为H＝6.6 m，不计空气阻力，求：
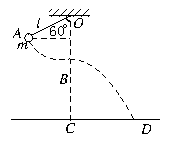
（1）摆球落地时的速度的大小.
（2）落地点D到C点的距离（g＝10 m／s2）.
答案
(1) vD＝10.8 m／s (2) 4 m
题目分析：（1）球从A到B受重力和线的拉力，只有重力做功，球从B到D 做平抛运动，也只有重力对球做功，故球从A到D运动的全过程中机械能守恒，取地面为参考面，则
mg（H－lcos60°）＝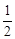
mvD2 （3分）
得 vD＝10.8 m／s （2分）
（2）在球从A到B的过程中，根据机械能守恒定律（取B点所在的水平面为参考面）得 mgl（1－cos60°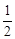）＝mvB2 （3分）
解得 vB＝4 m／s， （1分）
球从B点开始做平抛运动到D点时下落的高度为
h＝H－l＝5.0 m （1分）
则球做平抛运动的时间为 t＝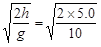
s＝1 s （2分）
球着地点D到C点的距离为 s＝vBt＝4×1 m＝4 m. （2分）
点评：做多过程问题时，受力分析是关键，根据受力分析判断运动性质，运动规律