问题
计算题
如图所示，一粗糙的水平轨道靠在半径为R="0.2" m的1/4光滑圆弧轨道右侧，光滑圆弧轨道固定，水平轨道处在光滑的水平面上，可自由滑动。一质量m="1" kg的滑块（可视为质点）从A点正上方H="3" m处自由下落经圆弧轨道最低点B进入水平轨道．滑块在水平轨道上滑行1 s后离开轨道。已知水平轨道质量M="5" kg，轨道面离地面高h="1.8" m，滑块与水平轨道间的动摩擦因数μ=0.5．（取g="10" m/s2）.求：
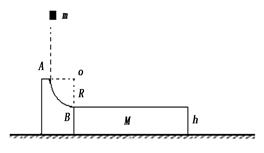
（1）滑块到达B点时对轨道的压力；
（2）水平轨道的长度；
（3）滑块落地时，它与水平轨道右端的水平距离。
答案
（1）330 N；（2）5 m；（3）1.2 m
题目分析：（1）滑块从最高点运动到B：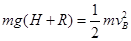
(1分)
在B点：
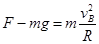(1分)
解得： F=" 330" N
滑块在B点对轨道的压力竖直向下，大小为330 N (1分)
（2） 滑块在水平轨道上运动，对滑块m：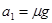
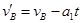(1分)
(1分)
对轨道M：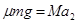
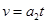(1分)
(1分)
由能量守恒定律有：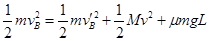
(2分)
解得，水平轨道长度：L=" 5" m (1分)
（3）滑块离开轨道后，滑块平抛运动：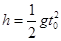
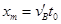(1分)
(1分)
轨道匀速运动：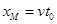
(1分)
滑块落地时，它与水平轨道右端的水平距离：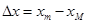
(1分)
解得：
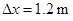(1分)