问题
计算题
如图所示，一个质量为0.6kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧AB的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)，并从最低点B通过一段光滑小圆弧滑上另一粗糙斜面CD。已知圆弧AB的半径R=0.9m,θ=600,B在O点正下方，斜面足够长，动摩擦因数u=0.5，斜面倾角为370，小球从p到达A点时的速度为4m/s。（g取10m/s2，cos37°=0.8，sin37°=0.6）问：
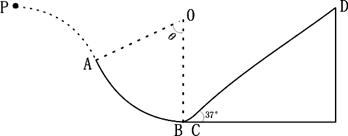
（1）P点与A点的水平距离和竖直高度
（2）小球在斜面上滑行的总路程
答案
(1) x=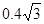
m；y=0.6m；（2）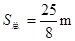
题目分析: （1）A点的水平分速度为：vAx= vAcos60°=2m/s，
竖直分速度为：vAy= vAsin60°=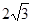
m/s，时间t= vAy/g=
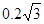s
P点与A点的水平距离x= vAxt=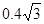m
P点与A点的竖直高度y=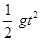
=0.6m
（2）设小球斜面向上运动的距离为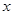
，则
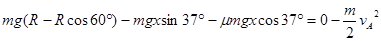
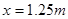再滑下时设过了A点，则
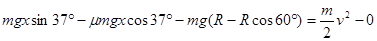
故小球不能过A点，只能来回摆动，最后停在B点，由能量守恒定律
得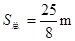： （1分）