问题
选择题
如图所示，在竖直平面内有一固定轨道，其中AB是长为R的粗糙水平直轨道，BCD是圆心为O、半径为R的3/4光滑圆弧轨道，两轨道相切于B点．在推力作用下，质量为m的小滑块从A点由静止开始做匀加速直线运动，到达B点时即撤去推力，小滑块恰好能沿圆轨道经过最高点C。重力加速度大小为g，取AB所在的水平面为零势能面。则小滑块
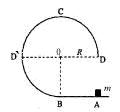
A．在AB段运动的加速度为2.5g
B．经B点时加速度为零
C．在C点时合外力的瞬时功率为mg
D．上滑时动能与重力势能相等的位置在直径DD′上方
答案
AD
题目分析：小滑块恰好能沿圆轨道经过最高点C，根据牛顿第二定律求出最高点的速度，通过动能定理求出经过B点的速度，从而求出B点的加速度，根据速度位移公式求出AB段的加速度大小。根据机械能守恒定律求出上滑时动能和重力势能相等的位置。由于小滑块恰好能沿圆轨道经过最高点C，在C点有：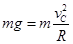
，解得
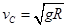，物体从B到C过程中，根据动能定理有：
解得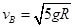
，根据匀加速的速度位移公式vB2＝2aR，所以物体在AB段匀加速运动的加速度为a=2.5g，故A正确；在B点时，合力的方向竖直向上充当向心力，则向心加速度
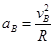=5g，故B选项错误；C点的速度方向与合力的方向垂直，所以合力的瞬时功率为0．故C错误。设物块上滑时动能与重力势能相等的位置据B的的高度为h，物块在圆弧轨道上滑的过程中机械能守恒，有：
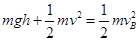，而
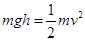，解得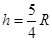
,故动能和重力势能相等的位置在
的上方，故D正确。