问题
计算题
如图所示，一不可伸长的轻绳上端悬挂于O点，下端系一质量m=1.0kg的小球。现将小球拉到A点（保持绳绷直）由静止释放，当它经过B点时绳恰好被拉断，小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上，已知绳长L=1.0m，B点离地高度H=1.0m，A、B两点的高度差h=0.5m，重力加速度g取10m/s2，不计空气阻力影响，求：
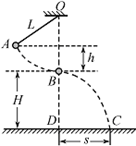
（1）地面上DC两点间的距离s；
（2）轻绳所受的最大拉力大小。
答案
（1）1.41m （2）20 N
（1）设小球运动至B点的速度为v，小球由A运动至B点的过程中，只有重力做功，根据动能定理有mgh=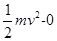
①
小球由B至C过程中，做平抛运动，设平抛运动的时间为t，根据平抛运动的规律
在水平方向上有：s=vt ②
在竖直方向上有：H=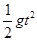
③
由①②③式联立，并代入数据解得：s=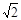
m=1.41m
（2）在小球刚到达B点绳断瞬间前，受重力mg和绳的拉力T作用，根据牛顿第二定律有：
T-mg=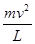
④
显然此时绳对小球的拉力最大，根据牛顿第三定律可知，绳所受小球的最大拉力为：T′=T⑤
由①④⑤式联立，并代入数据解得：T′=20N。
【考点定位】本题综合考查了圆周运动向心力公式、平抛运动规律、动能定理（或机械能守恒定律）、牛顿运动定律的应用问题，难度中等。