问题
计算题
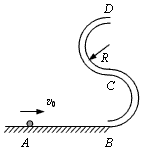
如图所示为“S”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道不可移动。弹射装置将一个小球(可视为质点)从A点以v0水平弹射向B点并进入轨道,经过轨道后从最高点D水平抛出,已知小球与地面AB段间的动摩擦因数μ=0.2,不计其他机械能损失,AB段长L=1.25 m,问:
(1)若圆的半径R=0.25m,v0至少多大才能使小球从D点抛出?
(2)若v0=9.22m/s,圆的半径R取何值时,小球从D点抛出后的水平位移最大(抛出后小球不会再碰到轨道)?
答案
解:(1)小球恰好能从A点运动到D点,根据动能定理
-μmgL-mg4R=0-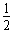 mv02
mv02
代入数据得v0=5m/s
(2)设D点时的速度为v
-μmgL-mg4R= mv2-
mv2-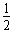 mv02 ①
mv02 ①
小球从D点抛出后做平抛运动,设水平位移为S,有
4R=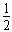 gt2 ②
gt2 ②
S=vt ③
联立①②③,得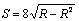
所以,当R=0.5m时,水平位移最大
