问题
计算题
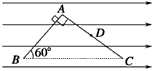
如图所示，BAC是光滑绝缘的“L”字形平面，倒置于水平匀强电场中BA⊥AC，D为AC的中点，BC与水平面平行，且∠B＝60°，AB＝l，有一带电荷量为＋q的滑块，质量为m，先由A端沿AB面无初速下滑，到达B端的速率为v0，再由A端沿AC面无初速下滑能到C端。试求：
（1）滑块到达D点的速度大小vD；
（2）假设滑块对C端没有压力，滑块的加速度多大。
答案
解：（1）设AB间的电压大小为U
从A→B，由动能定理得：mg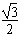
l－qU＝
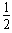mv02－0 ①
从A→D，由动能定理得：mghAD＋qUAD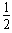＝mvD2－0 ②
又hAD＝
l，UAD＝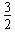
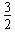UBA＝U ③
解①②③各式得：vD＝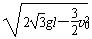
（2）滑块在C端受力分析如图
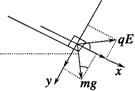
由FN＝0得：mgcos30°＝qEsin30° ④
又由牛顿第二定律得：qEcos30°＋mgsin30°＝ma ⑤
解④⑤得：a＝2g