问题
计算题
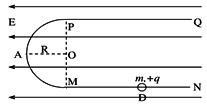
一绝缘“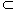
”杆由两段相互平行的足够长的水平直杆PQ、MN和一半径为R的光滑半圆环MAP组成，固定在竖直平面内。其中MN光滑，PQ杆是粗糙的，现将质量为M的带正电荷的小环套在MN杆上，小环所受的电场力为重力的1/2。
（1）若将小环由D点静止释放，刚刚好能停在P点，求DM间的距离。
（2）若将小环由M点右侧5R处静止释放，设小环与PQ杆间的动摩擦因数为μ，小环的最大静摩擦力和滑动摩擦力相等，求小环整个运动过程中克服摩擦力所做的功。
答案
解：（1）据动能定理qEx－2mgR=0－0
qE=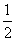
mg
联立解得x=4R
（2）若μmg≥qE（即μ≥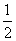
）
设小环到达P点右侧s1处静止
据动能定理qE(5R－s1)－mg·2R－fs1=0－0
f=μN=μmg
联立解得s1=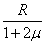
克服摩擦力做功W1=μmgs1=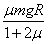
若μmg＜qE（即μ＜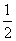
）
小环经过往复运动，最后在P点速度为0
据动能定理qE·5R－mg·2R－W2=0－0
克服摩擦力做功W2=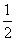
mgR