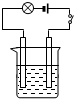
问题
计算题
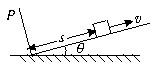
如图所示，斜面倾角为θ，质量为m的滑块距挡板P为s，以初速度v沿斜面上滑，滑块与斜面间的动摩擦因数为μ，滑块所受摩擦力小于滑块重力沿斜面的分力，若滑块每次与挡板相碰均无机械能损失，求滑块经过的路程有多大？
答案
解：由于滑块重力沿斜面向下的分力大于滑块所受摩擦力，所以可断定滑块最终将停靠在挡板处。从以v向上滑动至最终停下，设滑块经过的路程为l，则重力做正功，摩擦力做负功
解法一：此过程重力对滑块做功WG＝mgssinθ
摩擦力做功Wf＝-μmglcosθ
对滑块由动能定理，有：mgssinθ－μmglcosθ＝0－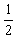
mv2
解得l＝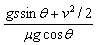
解法二：由能量转化与守恒求解，此过程滑块机械能的减少ΔE1＝mgssinθ＋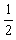
mv2，克服摩擦力做功转化的内能ΔE2＝μmgcosθ·l，由能量守恒定律有ΔE1＝ΔE2
即mgssinθ＋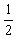
mv2＝μmglcosθ
同样可解出l