问题
填空题
矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若OE:ED=1:3,AE=
|
答案
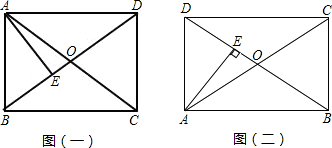
如图(一)所示,
AB是矩形较短边时,
∵矩形ABCD,
∴OA=OD=
BD;1 2
∵OE:ED=1:3,
∴可设OE=x,ED=3x,则OD=2x
∵AE⊥BD,AE=
,3
∴在Rt△OEA中,x2+(
)2=(2x)2,3
∴x=1
∴BD=4.
当AB是矩形较长边时,如图(二)所示,
∵OE:ED=1:3,
∴设OE=x,则ED=3x,
∵OA=OD,
∴OA=4x,
在Rt△AOE中,x2+(
)2=(4x)2,3
∴x=
,5 5
∴BD=8x=8×
=5 5
.8 5 5
故答案为:4或
.8 5 5
