问题
计算题
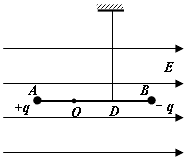
如图所示，绝缘轻杆长L＝0.9m，两端分别固定着带等量异种电荷的小球A、B，质量分别为mA＝4×10-2kg，mB＝8×10-2kg，A球带正电，B球带负电，电荷量q＝6.0×10-6C。轻杆可绕过O点的光滑水平轴转动，OB＝2OA。一根竖直细线系于杆上OB中点D使杆保持水平，整个装置处在水平向右的匀强电场中，电场强度E＝5×104N/C。不计一切阻力，取g＝10m/s2，求：
（1）细线对杆的拉力大小；
（2）若将细线烧断，当轻杆转过90°时，A、B两小球电势能总的变化量；
（3）细线烧断后，在杆转动过程中小球A的最大速度。
答案
解：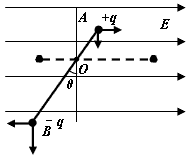
（1）根据有固定转动轴物体的平衡条件，有
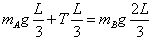
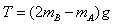＝（2×8×10-2－4×10-2）×10＝1.2N
（2）杆转过90°时，电场力对两带电小球做正功，电势能减少
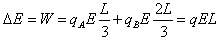＝6.0×10-6×5×104×0.9＝0.27J
（3）当力矩的代数和为零时，B球的速度达到最大
＝
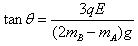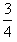
θ＝37°
由动能定理：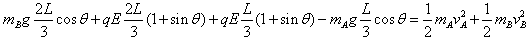
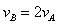
联立求得：vA＝2m/s