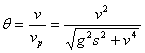问题
计算题
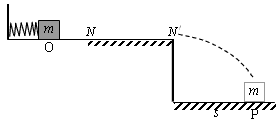
如图所示,质量为m的木块压缩轻质弹簧静止在O点,水平面ON段光滑,长为L的NN'段粗糙,木块与NN'间的动摩擦因数为μ。现释放木块,若木块与弹簧相连接,则木块最远到达NN'段中点,然后在水平面上做往返运动,且第一次回到N时速度大小为v;若木块与弹簧不相连接,木块与弹簧在N点即分离,通过N'点时以水平速度飞出,木块落地点P到N'的水平距离为s。求:
(1)木块通过N'点时的速度;
(2)木块从O运动到N的过程中弹簧弹力做的功;
(3)木块落地时速度vp的大小和方向。
答案
解:(1)木块从N到NN'中点,再回到N点,此过程弹簧弹力做功代数和为零,克服摩擦力做的功为W克;若木块与弹簧不相连接,木块从N到达N'过程中,弹簧弹力不做功,克服摩擦力做的功也为W克,又因为两种情况木块到达N时的速度相同,所以到达N'的速度v'应等于第一次回到N时速度v,即v'=v
(2)木块从O运动到N的过程中弹簧弹力做的功为W
W-W克=mv2/2
W=mv2/2+mgL
(3)木块落地时速度为vp
t=s/v,h=gt2/2=gs2/2v2
mgh=mvp2/2-mv2/2
得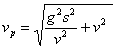
vp与水平方向夹角为θ,cos