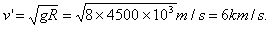问题
计算题
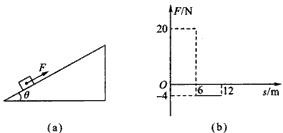
半径R=4 500 km的某星球上有一倾角为θ=30°的固定斜面。一质量为m=l kg的小物块在力F作用下从静止 开始沿斜面向上运动，力F始终与斜面平行，如图(a)所示。已知小物块和斜面问的动摩擦因数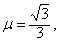
力F随位移s变化的规律如图(b)所示（取沿斜面向上的方向为正），那么小物块运动12 m时速度恰好为零，试求：
（1）该星球表面上的重力加速度；
（2）该星球表面抛出一个物体，为使该物体不再落回该星球，至少需要多大速度？
答案
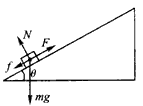
解：（1）假设该星球表面的重力加速度为g，根据动能定理，小物块在力F1作用过程中有：
①
N=mgcosθf=μN ②
小物块在力F2作用过程中有：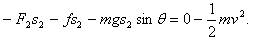
③
由题图可知：F1=20 N，s1=6 m；F2=4 N，s2=6 m
由①②③式得：g=8 m/s2
（2）要使抛出的物体不再落回星球，物体的最小速度v'必须满足：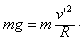
所以