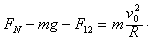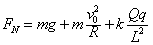阅读理解。
A
Liu Tao: I want to write a letter.
Mum: Who do you want to write to?
Liu Tao: Mike. I want to be his pen-friend. I saw his name in the newspaper yesterday afternoon.
Mum: Who's Mike?
Liu Tao: He's an English boy. He lives in London.
根据上下文内容，填入适当的单词。
Mike is from____and lives in London. Liu Tao to write a letter him. He about Mike in
the newspaper yesterday afternoon. Liu Tao wants to Mike's pen-friend.
B
Bob and Jim worked in the same factory. One day Jim borrowed（借）ten dollars from Bob, but then Jim
left his work and went to work in another town, so he didn't give back the money. Bob didn't see Jim for a year.
Later, he knew from a friend where Jim was. So one day he went there to see him late in the evening. When he
got to Jim's room, he saw his shoes near the door. "Well, he must be in. " he thought. He knocked at the door.
There was no answer. He knocked again and said, "I know you are in, Jim. Your shoes are out here. "
判断下列句子是否与短文意思相符，相符的写“T”，不相符的写“F”。
( ) 1. Bob and Jim worked in the same school.
( ) 2. Bob got some money from Jim.
( ) 3. Jim didn't give back the money when he went to another town.
( ) 4. Jim didn't meet Bob for two years.
( ) 5. When Bob knocked at the door, Jim opened.
C
The Road family often does housework together at the weekends. Pam often cleans bedrooms. Her father
buys groceries(食品杂货)for the next week. Her mum washes the clothes. John, Pam's brother, helps to cut
grass in their garden.
The Roads often ride a bike to the park nearby. In the park, they can play basketball and football. They
always have a good time there.
It is happy when a family works and plays together.
根据短文内容选择正确答案。
( ) 1. How many people are there in the Road family?
A. Two. B. Three. C. Four. D. Five.
( ) 2. The Road family likes to .
A. go on a picnic B. go shopping C. have a rest D. go to the park
( ) 3. When the family work together, they feel
A. tired B. happy C. angry D. sad
( ) 4. cuts the grass in the garden.
A. Father B. Mother C. Pam D. John
( ) 5. A good title（标题）for the passage is .
A. A family works and plays together B. Cleaning the rooms
C. A big family D. Pam and her parents
圆弧轨道的最低点C相切，已知圆弧的半径为R，现把质量为m，带电量为+Q的小球（可视为质点）由圆弧的最高点M静止释放，到最低点C时速度为v0。已知静电力常量为k，现取D为电势零点，求：
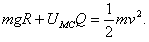
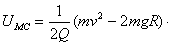
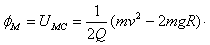
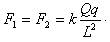
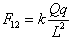，且方向是竖直向下的
