问题
计算题
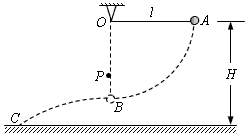
一长l=0.80m的轻绳一端固定在O点，另一端连接一质量m=0.10kg的小球，悬点O距离水平地面的高度H=1.00m。开始时小球处于A点，此时轻绳拉直处于水平方向上，如图所示。让小球从静止释放，当小球运动到B点时，轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失，取重力加速度g=10m/s2。
（1）小球运动到B点时的速度大小？
（2）绳断裂后球从B点抛出并落在水平地面的C点，求C点与B点之间的水平距离？
（3）若轻绳所能承受的最大拉力Fm=9.0N，求钉子P与O点的距离d应满足什么条件？
答案
解：（1）设小球由A运动到B点时的速度大小vB，由动能定理得
①
解得小球运动到B点时的速度大小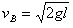
=4.0 m/s ②
（2）小球从B点做平抛运动，由运动学规律得
③
④
解得C点与B点之间的水平距离
=0.80m ⑤
（3）若轻绳碰到钉子时，轻绳拉力恰好达到最大值Fm，由牛顿定律得
⑥
⑦
由以上各式解得d=0.60m ⑧
因此钉子P与O点的距离d应满足条件0.60m＜d＜0.80m ⑨