问题
计算题
如图所示,矩形盒B的质量为M,放在水平面上,盒内有一质量为m的物体A,A与B、B与地面间的动摩擦因数分别为μ1、μ2,开始时二者均静止,现瞬间使物体A获得一向右的水平速度v0,以后物体A在与盒B的左右壁碰撞时,B始终向右运动,当A与B最后一次碰撞后,B停止运动,A则继续向右滑行距离x后也停止运动,求盒B运动的时间t。

答案
解:以物体A、盒B组成的系统为研究对象,它在水平方向所受的外力就是地面对盒B的滑动摩擦力,而A与B间的摩擦力、A与B碰撞时的相互作用力均是内力
设B停止运动时A的速度为v,且假定向右为正方向,对由物体A和盒B组成的系统应用动量定理得:
-μ2(m+M)gt=mv-mv0 ①
当B停止运动后,对A应用动能定理得: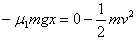 ②
②
由①②两式解得B运动的时间为:
