问题
计算题
轨道ABCD由粗糙的斜面轨道AB和光滑圆弧轨道BCD组成。圆弧轨道BCD半径R=1m,在B点与斜面轨道AB相切;C点是圆弧轨道的最低点,D点的切线沿竖直方向;斜面轨道与水平面的夹角θ=37°,物块与斜面间的动摩擦因数μ=0.3。在D点的正上方有一厚度不计的旋转平台,沿平台的一条直径上开有两个小孔P、Q,两孔离轴心等距离,旋转时两孔均能达到D点的正上方。一质量m=0.5kg的物块(视为质点)从斜面上A点由静止释放,到达C点时对轨道的压力N=65N,到达D点后恰好无碰撞的穿过小孔P,为了使物块能从小孔Q落下(不计空气阻力,重力加速度g=10m/s2,取sin37°=0.6,cos37°=0.8),求:
(1)物块到达C点时的速度(结果可用根式表示);
(2)AB的长度L(结果可用分数表示);
(3)平台的角速度ω应满足的条件。
答案
解:(1)在C点,根据牛顿定律有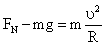
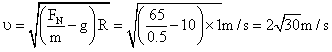
(2)由动能定理,有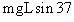 °+
°+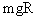 (1-cos37°)-
(1-cos37°)-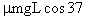 °
°
解得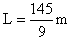
(3)设小球到达D点时的速度是vD,则在物块由C到D过程中,有
解得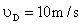
物块越过孔后做初速度为10m/s、加速度为-g的匀变速运动,由运动学公式有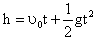

可得t=2s
根据θ=ωt得ω应满足
