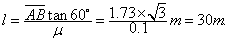问题
计算题
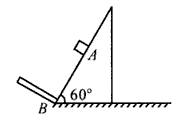
如图所示，一质量为m的物块从倾角为60°的斜面上的A点由静止释放，下滑到B点时与挡板碰撞，碰撞后物块以碰前的速率反弹沿斜面向上滑动．若物块与斜面间的动摩擦因数μ=0.1，AB=1.73 m.
(1)试分析物块最终停在何处；
(2)求物块在全过程中运动的路程．
答案
解：
(1)物块下滑过程中克服摩擦力做功，一部分机械能转化为内能，反弹后继续上升，上升过程中仍克服摩擦力做功，机械能继续减少，物块上升到最高点的高度小于下滑时的高度．之后，物块再下滑重复上一过程，但返回到最高点的高度继续减小，最终物块停在挡板处．
(2)在物块运动的全过程中，重力做功WG=mg
sin60°（与路径无关）．滑动摩擦力做的功等于物块受到的滑动摩擦力（Fμ=μmgcos60°）与运动路程的乘积，即W1=-μmglcos60°．物块由初态的静止到最终静止，动能的变化△Ek =0.
对物块运动的全过程运用动能定理得
mg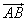
sin60°-μmglcos60°=0.
所以物块在全过程中运动的路程
