问题
计算题
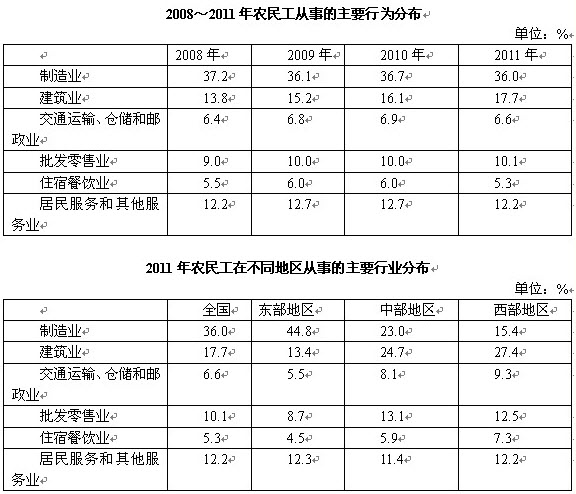
如图所示,空间存在着电场强度为E=2.5×102N/C、方向竖直向上的匀强电场,一长为L=0.5m的绝缘细线,一端固定在O点,一端拴着质量m=0.5kg、电荷量q= 4×10-2 C的小球。现将细线拉直到水平位置A,使小球由A静止释放,则小球能运动到最高点。不计阻力。取g=10m/s2。求:
(1)小球的电性。
(2)细线在最高点受到的拉力。
(3)若小球刚好运动到最高点时细线断裂,则细线断裂后小球继续运动到与O点水平方向距离为细线的长度L时,小球距OA所在水平面的高度。

答案
解:(1)由小球运动到最高点可知,小球带正
(2)设小球运动到最高点时速度为v,对该过程由动能定理有
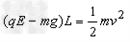 ①
①
在最高点对小球由牛顿第二定律得,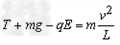 ②
②
由①②式解得,T=15N
(3)小球在细线断裂后,在竖直方向的加速度设为a,则
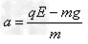 ③
③
设小球在水平方向运动L的过程中,历时t,则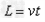 ④
④
设竖直方向上的位移为s,则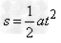 ⑤
⑤
由①③④⑤解得,s=0.125m
小球距O点高度为s+L=0.625m