问题
计算题
一固定的斜面，倾角为45°，斜面长L=2.0 m，在斜面下端有一与斜面垂直的挡板。一质量为m的滑块，从斜面的最高点由静止沿斜面滑下，下滑到斜面最底端与挡板发生碰撞（碰撞前后能量没有损失）。已知滑块与斜面间的动摩擦因数μ=0.2。求：
(1)滑块第1次到达斜面最底端时的速度大小；
(2)滑块第1次与挡板碰撞反弹后沿斜面上升的最大距离与第一次下滑的距离之比；
(3)此滑块从开始运动到与挡板发生第5次碰撞前的过程中所运动的总路程。
答案
解：(1)由动能定理得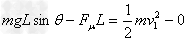
①
且Fμ=μmgcosθ ②
由①②得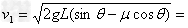
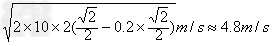
(2)滑块向上运动由动能定理得
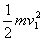③
由方程①②③得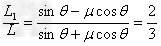
(3)令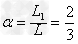
，则L1=αL
同理第2次碰撞后上升的距离为L2=αL1=α2L
第3次碰撞后上升的距离为L3=αL2=α3L
……
第1次碰撞前通过的路程s1=L
第2次碰撞前通过的路程s2=L+2L1=L+2αL
第3次碰撞前通过的路程s3=L+2L1+2L2=L+2αL+2α2L
……
第5次碰撞前通过的路程
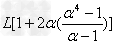
代入数值得s5=8.42 m