问题
计算题
如图1所示，一质量为m＝1 kg的物块静止在粗糙水平面上的A点，从t＝0时刻开始，物块受到按如图2所示规律变化的水平力F作用并向右运动，第3 s末物块运动到B点时速度刚好为0，第5 s末物块刚好回到A点，已知物块与粗糙水平面之间的动摩擦因数μ＝0.2，求(g取10 m/s2)：
(1)A与B间的距离；
(2)水平力F在5 s内对物块所做的功。
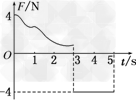
图1 图2
答案
解：(1)在3 s～5 s内物块在水平恒力F作用下由B点匀加速运动到A点，设加速度为a，A与B间的距离为x，则
F－μmg＝ma
a＝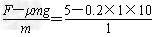
m/s2＝2 m/s2
x＝
at2＝4 m
即A与B间的距离为4 m
(2)设整个过程中F做的功为WF，物块回到A点时的速度为vA，由动能定理得：
WF－2μmgx＝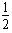
mvA2
vA2＝2ax
由以上两式得WF＝2μmgx＋max＝24 J