问题
计算题
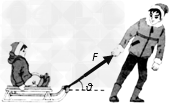
如图所示，已知小孩与雪橇的总质量为m=20 kg，静止于水平冰面上的A点，雪橇与冰面间的动摩擦因数为μ=0.1。（g取10m/s2）
（1）妈妈先用30N的水平恒力拉雪橇，经8秒到达B点，求A、B两点间的距离L。
（2）若妈妈用大小为30N，与水平方向成37°角的力斜向上拉雪橇，使雪橇从A处由静止开始运动并能到达（1）问中的B处，求拉力作用的最短距离。（已知cos37°=0.8 ，sin37°= 0.6）
（3）在第（2）问拉力作用最短距离对应的运动过程中，小孩与雪撬的最大动能为多少？
答案
解：（1）对小孩进行受力分析，由牛顿第二定律得：
F-μmg=ma
a=0.5m/s2
L=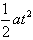
L=16 m
（2）设妈妈的力作用了x距离后撤去，小孩到达B点的速度恰好为0
方法一：由动能定理得Fcos37°x-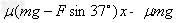
（L -x）= 0
方法二：Fcos37°-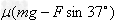
=ma1
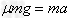2
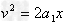
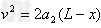
x=12.4 m
（3）小孩和雪撬在妈妈撤去力时的动能最大
方法一：由动能定理得Fcos37°x-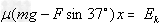
方法二：由动能公式得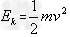
Ek=72J (数值在71.9至72之间均可)