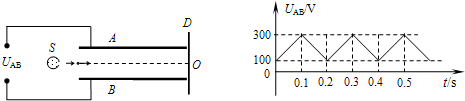
一个水平放置的平行板电容器,极板长L=20cm、板间距d=2cm.在两极板AB间加上如图所示的脉冲电压(A板电势高于B板电势),板右侧紧靠电容器竖直放置一个挡板D,板左侧有一个连续发出相同带电微粒的粒子源S,所产生的带电微粒质量m=2×10-8kg、电荷量q=+2.5×10-7C,且正好沿两极板正中间平行于极板的速度v0=500m/s射入电容器,由于粒子通过电容器的时间极短,可认为此过程中AB两板间电压不变,(微粒重力不计).求:
(1)当t=0时刻进入平行板间的微粒最后击中挡板上的位置;
(2)哪些时刻进入平行板间的微粒击中挡板时的动能最大,这些粒子在电场中动能变化多大.
(1)当t=0时刻加在电容两极板间的电压U0=100V,粒子在入射方向上偏移的距离为
y=1 2
(qU0 md
)2=L v0
×1 2
(2.5×10-7×100 2×10-8×0.02
)2=5×10-3(m)0.2 500
即t=0时刻,通过电容器的微粒,击中挡板中点O的下方0.5cm处.
(2)当微粒偏离入射方向的距离为
d时的微粒击中挡板时的动能最大.1 2
设此时加在AB两板上的电压为Ux,则
d=1 2 1 2
(qUx md
)2L v0
解得 Ux=
=200(V)md2 v 20 qL2
从图中可知 当t=0.05+0.1n(s)(其中n=0、1、2、3、…)时刻加在电容器两极板间的电压为200V,这些时刻进入电容器并击中挡板的微粒动能最大.
这些微粒在电场中的动能变化为△Ek=
qUx=1 2
2.5×10-7×200=2.5×10-5(J)1 2
答:
(1)当t=0时刻进入平行板间的微粒最后击中挡板上的位置是挡板中点O的下方0.5cm处.;
(2)当t=0.05+0.1n(s)(其中n=0、1、2、3、…)时刻进入平行板间的微粒击中挡板时的动能最大,这些粒子在电场中动能变化为2.5×10-5(J).
