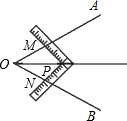
(1)班同学上数学活动课,利用角尺平分一个角(如图所示).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由;
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件,
∵只有OP=OP,PM=PN不能判断△OPM≌△OPN;
∴就不能判定OP就是∠AOB的平分线;
方案(Ⅱ)可行.
证明:在△OPM和△OPN中,
,OM=ON PM=PN OP=OP
∴△OPM≌△OPN(SSS),
∴∠AOP=∠BOP(全等三角形对应角相等);
∴OP就是∠AOB的平分线.
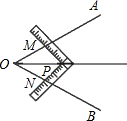
(2)当∠AOB是直角时,此方案可行;
∵四边形内角和为360°,∠OMP=∠ONP=90°,∠MPN=90°,
∴∠AOB=90°,
∵PM=PN,
∴OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上),
当∠AOB不为直角时,此方案不可行;
因为∠AOB必为90°,如果不是90°,则不能找到同时使PM⊥OA,PN⊥OB的点P的位置.
