问题
计算题
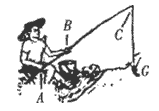
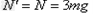如图（a）所示，一质量为m的滑块（可视为质点）沿某斜面顶端A由静止滑下，已知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图（b）所示。斜面倾角为37°，长为L，有一半径为R＝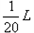
的光滑竖直半圆轨道刚好与斜面底端B相接，且直径BC与水平垂直，假设滑块经过B点时没有能量损失。求：
（1）滑块滑至斜面中点时的加速度大小；
（2）滑块滑至斜面底端时的速度大小；
（3）试分析滑块能否滑至光滑竖直半圆轨道的最高点C。如能，请求出在最高点时滑块对轨道的压力；如不能，请说明理由。
答案
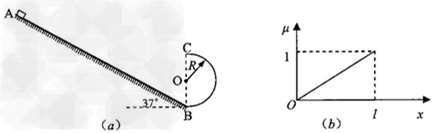
解：（1）滑块滑至斜面中点时，由图b可知，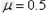
则对滑块：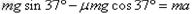
代入数据解得：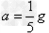
（2）滑块由顶端滑至底端，由动能定理得：
由图b的物理意义得：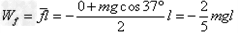
解得：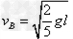
（3）设滑块能运动到C点，则从B到C，由动能定理：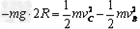
解得：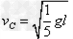
如滑块恰好滑到C点：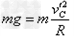
解得：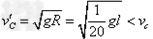
所以滑块能够到达C点
当滑块滑到C点时：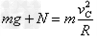
解得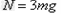
由牛顿第三定律得滑块在C点时对轨道的压力