问题
问答题
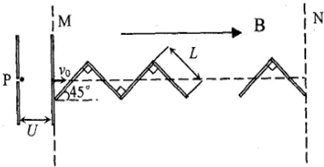
如图一个质量为m、电量为e的静止质子,经电压为U的电场加速后,射入与其运动方向一致的磁感应强度为B的匀强磁场MN区域内.在MN内有n块互成直角、长为L的硬质塑料板(不导电,宽度很窄,厚度不计).
(1)求质子进入磁场时的速度v0
(2)若质子进入磁场后与每块塑料板碰撞后均没有能量损失且满足反射原理.求质子穿过磁场区域所需的时间t
答案
(1)根据动能定理:eU=
m1 2
得v0=v 20 2eU m
故质子进入磁场时的速度为v0=
.2eU m
(2)质子打到第一块板上后速度与原速度方向垂直,由于没有能量损失,仍以大小为v0的速度垂直磁场方向,以半径R在垂直于磁场的平面内做匀速圆周运动,转动一周后打到第一块板的下部.由于不计板的厚度,所以质子从第一次打到板后到第二次打到板运动时间为质子磁偏转周期T
根据牛二定律evB=
和运动学T=mv02 R
得T=2πR v0 2πm eB
质子在磁场中共碰到n块板,做圆周运动所需要时间为t2=nT
子进入磁场中,在v0方向的总位移s=nLsin45°
时间为t1=s v0
则t=t1+t2=nL 2
+m eU 2nπm eB
故质子穿过磁场区域所需的时间t为nL 2
+m eU
.2nπm eB

