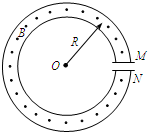
如图所示为一种获得高能粒子的装置.环形区域内存在垂直纸面向外,大小可调的匀强磁场.M、N为两块中心开有小孔的极板,每当带电粒子经过M、N板时,都会被加速,加速电压均为U;每当粒子飞离电场后,M、N板间的电势差立即变为零.粒子在M、N间的电场中一次次被加速,动能不断增大,而绕行半径R不变(M、N两极板间的距离远小于R).当t=0时,质量为m,电荷量为+q的粒子静止在M板小孔处;M、N间间距很小,粒子在M、N间的电场中的加速时间可忽略不计;
(1)求粒子绕行n圈回到M板时的动能En;
(2)为使粒子始终保持在圆轨道上运动,磁场必须周期性递增;求粒子绕行第n圈时磁感应强度B的大小;
(3)求粒子绕行n圈所需总时间tn.
(1)粒子绕行一圈动能的增量为qU,绕行n圈所获得的总动能:En=nqU
(2)因为nqU=
m1 2 v 2n
qBnvn=m v 2n R
得Bn=1 R 2nmU q
(3)粒子做半径为R的匀速圆周运动,每一圈所用时间为
,2πR v
由于第一圈速度不同,所以每一圈所需时间也不同
第一圈:qU=
m1 2
v1=v 21 2qU m
第二圈:2qU=
m1 2
v2=v 22 2?2qU m
…
第n圈的速度 vn=n?2qU m
故绕行n圈所需总时间tn=t1+t2+t3+…+tn=
+2πR v1
+…+2πR v2
=2πR2πR vn
(1+m 2qU
+1 2
…+1 3
)1 n
答:(1)求粒子绕行n圈回到M板时的动能nqU;
(2)粒子绕行第n圈时磁感应强度B的大小Bn=1 R
;2nmU q
(3)求粒子绕行n圈所需总时间tn=2πR
(1+m 2qU
+1 2
…+1 3
).1 n
