问题
问答题
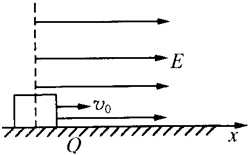
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同,在O处放一个质量m=10g带负电荷的绝缘小物块,其带电量q=5×10-8 C.小物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.试求:
(1)小物块沿x轴正方向运动离O点的最远距离;
(2)小物块最终停止时的位置.
答案
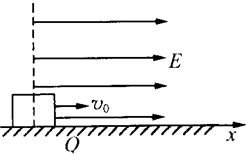
(1)当物块沿x轴正方向运动时,受到沿x轴负方向的电场力F和动摩擦力f.电场力大小为F=Eq,滑动摩擦力大小为f=μFN=μmg.
设物块沿x轴正方向运动离O点的最远距离为s,此过程中由动能定理得
-(F+f)s=-
mv021 2
联立解得 s=
=0.4mmv02 2(qE+μmg)
(2)由于F>f,当物块运动到沿x轴正方向运动离O点的最远距离时,又返回向x轴负方向运动,设最终停止时在侧s'处.
在物块向x轴负方向运动的过程中,由动能定理得:
(F-f)s-fs'=0
解得 s′=
s=0.2mF-f f
答:(1)小物块沿x轴正方向运动离O点的最远距离为0.4m;
(2)小物块最终停止时的位置在O点左侧0.2m处.
