如图所示,粒子源S可以不断地产生质量为m、电荷量为+q的粒子(重力不计).粒子从O1孔漂进一个水平向右的加速电场(初速不计),再经小孔O2垂直射入相互正交的匀强电场和匀强磁场区域,电场强度大小为E,磁感应强度大小为B1,方向如图.边长为L的长方体ABCDEFGH处在匀强磁场中,磁感应强度大小为B2,方向与ADHE平面垂直,由A指向B.长方体中HFC是一块三角形的硬质塑料板,如图所示.
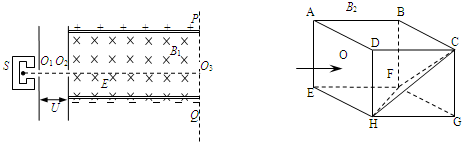
(1)若要粒子源射出的粒子能沿O2O3直线运动,并垂直于PQ边射出电磁复合场,加速电压U应多大?
(2)如果粒子从O3点射出电磁复合场后,再垂直ADHE平面并从该平面的正中心O点射入长方体中,恰好在HFC三角形硬质塑料板的CF边与板相碰,假设粒子与板相碰后,速度大小不变,方向变化遵守光的反射定律,那么若要粒子与板发生第一次碰撞后就能沿BCGF平面水平射出长方体,则磁感应强度B2应为多大?若要粒子与板发生第一次碰撞后不能从ABFE平面射出长方体,则磁感应强度B2至少应多大?
(1)粒子在相互正交的匀强电场和匀强磁场区域中做直线运动,则
qvB1=qE
故v=E B1
粒子在加速电场中加速时,由动能定理得:
qU=
mv2 1 2
U=
=mv2 2q mE2 2q B 21
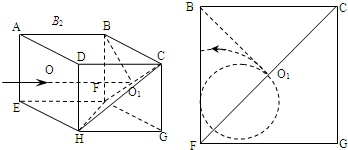
(2)粒子在CF边的中点O1与塑料板碰撞后在BCGF平面内沿O1B方向反弹,并在BCGF平面内内做圆周运动.
若要粒子能从ABFE所在的平面水平射出正立方体,粒子的运动轨迹必与BF垂直,
故粒子做圆周运动的圆心必在F点,圆周运动的半径R=
CF=1 2
L. 2 2
由牛顿第二定律得:qvB2=mv2 R
故有:B2=mv qR
解得 B2=
mE2 qB1L
若要粒子不能从ABFE所在的平面射出正立方体,如图所示,则粒子做圆周运动的圆心必在O1F上,设圆周运动的半径为r. 则
r+rcos45°=L 2
即r=L 2+ 2
同理解得B2=
,即B2至少为(2+
)mE2 qB1L (2+
)mE2 qB1L
答:(1)若要粒子源射出的粒子能沿O2O3直线运动,并垂直于PQ边射出电磁复合场,加速电压U应;
(2)如果粒子从O3点射出电磁复合场后,再垂直ADHE平面并从该平面的正中心O点射入长方体中,恰好在HFC三角形硬质塑料板的CF边与板相碰,假设粒子与板相碰后,速度大小不变,方向变化遵守光的反射定律,那么若要粒子与板发生第一次碰撞后就能沿BCGF平面水平射出长方体,则磁感应强度 B2=
;若要粒子与板发生第一次碰撞后不能从ABFE平面射出长方体,则磁感应强度B2至少应为
mE2 qB1L
.(2+
)mE2 qB1L
