搜题请搜索小程序“爱下问搜题”
问题 问答题

1932年，劳伦斯和利文斯设计出了回旋加速器．回旋加速器的工作原理如图所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计．磁感应强度为B的匀强磁场与盒面垂直．A处粒子源产生的粒子，质量为m、电荷量为+q，在加速器中被加速，加速电压为U．加速过程中不考虑相对论效应和重力作用．

（1）求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比；

（2）求粒子从静止开始加速到出口处所需的时间t；

（3）实际使用中，磁感应强度和加速电场频率都有最大值的限制．若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm，试讨论粒子能获得的最大动能Ekm．

答案

（1）设粒子第1次经过狭缝后的半径为r1，速度为v1

qU=

1
2
mv12

qv1B=m

v21
r1

解得  r1=

1
B
2mU
q

同理，粒子第2次经过狭缝后的半径  r2=

1
B
4mU
q

则 r2：r1=

2
：1．

（2）设粒子到出口处被加速了n圈

2nqU=
1
2
mv2
qvB=m
v2
R
T=
2πm
qB
t=nT

解得  t=

πBR2
2U
．

（3）加速电场的频率应等于粒子在磁场中做圆周运动的频率，即f=

qB
2πm

当磁场感应强度为Bm时，加速电场的频率应为fBm=

qBm
2πm

粒子的动能EK=

1
2
mv2

当fBm≤fm时，粒子的最大动能由Bm决定qvmBm=m

v2m
R

解得Ekm=

q2
B2m
R2
2m

当fBm≥fm时，粒子的最大动能由fm决定vm=2πfmR解得 EKm=2π2m

f2m
R2

答：（1）r2：r1=

2
：1 （2）t=
πBR2
2U
 （3）当fBm≤fm时，EKm=
q2
B2m
R2
2m
；当fBm≥fm时，EKm=2π2m
f2m
R2．

阅读理解与欣赏
上帝只给他一只老鼠
　　①这是一位孤独的年轻画家，除了理想，他一无所有。
　　②为了理想，他毅然出门远行，来到堪萨斯城谋生。起初他到一家报社应聘，想替他们工作。编辑部周围有较好的艺术氛围，这也正是他所需要的，但主编阅读了他的作品后大摇其头，认为作品缺乏新意，不予录用。这使他感到万分失望和颓丧，和所有出门打天下的年轻入一样；他初尝了失败的滋味。
　　③后来，他终于找到了一份工作，替教堂作画。可是报酬极低，他无力租用画室，只好借用一家废弃的车库作为临时的办公室。他每天就在这充满汽油味的车库辛勤地工作到深夜。没有比现在更艰苦的了，他想。
　　④尤其令人提烦的是，每天熄灯睡觉时，就能听到老鼠吱吱的叫声和在地板上的跳跃声。为了明天有充足的精力去工作，他忍耐了。不过，好歹有一只老鼠与他为伴。他感到自己并不孤单。也许是太累了，他一沾着地板就能呼呼大题。
　　⑤那只小老鼠一次次出现，不只是在夜果。、他从来没有伤害过它，甚至连吓唬都没有。磨难己经使他具备大艺术家所具有的的悲天悯人的情怀。就这样，一名贫困的画家接纳了一只小老鼠，与它共处一室，倒也觉得这个荒弃的车库充满生机。小老鼠在地板上做着各种运动，表演精彩的杂技。而他作为唯一的观众，则奖给它一点点面包屑。渐渐地；他们互相信任，彼此便一点点靠近。老鼠先是离他较远，见他没有伤害它的意思，便一点点靠近。最后，老鼠竟然大胆地爬上他工作的画板，并在上面有节奏地跳跃、而他呢，决不会去赶走它，而是默默地享受与它亲近的情意。
　　⑥信赖，往往创造出美好的境界。
　　⑦不久，年轻的画家离开堪萨斯城，被介绍到好莱坞去制作一部以动物为主的卡通片。这是他好不容易得到的一次机会，他似乎看到理想的大门开了一道缝。但不幸得很，他再次失败了，不但因此穷得毫无分文，并且再度失业。
　　⑧多少个不眠之夜他在黑暗里苦苦思索，他怀疑自己的天赋，怀疑自己真的一文不值，他在思索着自己的出路、终于在某天夜里，就在他潦倒不堪的当儿，他突然想起了堪萨斯城车库里那只爬到他画板上跳跃的老鼠，灵感就在那个暗夜里闪了一道耀眼的光芒。他迅速爬起来，拉亮灯，支起画架，立刻画了一只老鼠的轮廓。
　　⑨有史以来，最伟大的动物卡通形象——米老鼠就这样平凡地诞生了。灵感只青睐那些勤于思考的头脑。
　　⑩这位年轻的画家就是后来的美国最负盛名的人物之——-才华横溢的沃特·迪斯尼先生。他创造了风靡全球的米老鼠。谁能想到，在那间充满汽油味的车库里曾经生活过的一只小老鼠是世界上最负盛名的影片的祖宗。米老鼠足迹所至，所受到的欢迎让许多明星望尘莫及，也让沃特·迪斯尼先生名噪全球。
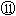　　堪萨斯城那间充满汽油味的车库，沃特·迪斯尼先生后来说，至少要值一百万美元。其实那里没有什么，只有一只老鼠，那是上帝给他的，上帝给谁都不会太多。
1、本文采用一人称的写法，按________的记叙顺序叙事。．
2、根据迪斯尼成功前的有关情节填写下表。
时间
经历
结果
起初
 
 
 
 
创作进入新的境界
 
被介绍到好莱坞制作卡通片
3、迪斯尼对小老鼠的感情经历过哪些变化？请从④⑤第段中找出词语填写。
厌烦→_____________→______________→_________________→亲近
4、迪斯尼取得成功的最主要的原因是（      ）
A、曾与一只老鼠朝相处
B、屡遭挫折，饱尝痛苦
C、勤于思考的头脑产生灵感
D、困顿之中找到捷径
5、作者为什么要详写迪斯尼与小老鼠相处的情节？请简要分析。
_________________________________________________________
6、揣摩文中画线句“信赖，往往创造出美好的境界”简答。
这句话在文中结构上的作用是：___________________________________
信赖使迪斯尼创造出怎样的“美好的境界”？
_______________________________________________________________
7、迪斯尼的挫折，灵感和成功，使你联想到时哪些名言名句或事例？请按提示作答。
挫折：_________________________________________________________
灵感：_________________________________________________________
成功：_________________________________________________________
查看答案
多项选择题

化学纤维在后处理牵伸中之所以采用分段牵伸，而不是一次牵伸完成主要是为了（）。

A、改善纤维的断裂伸长

B、降低牵伸中纤维的牵伸应力

C、降低牵伸过程中的能耗

D、减少牵伸过程中产生的毛丝
查看答案