如图所示,大量质量为、电量为的带电粒子(不计重力),由静止开始经电场加速后沿水平方向从P点进入的匀强磁场,不计各粒子之间的作用力.已知磁感应强度为B,磁场的两边界线竖直且上下足够长,宽度为.回答下列问题:
(1)加速电场的电压为U0时,粒子刚好能从磁场的右边界穿过,求U0=?
(2)若在P点加一个速度散射器(可使粒子速度方向变化,而不改变速度大小),使粒子从P点沿各个方向射入磁场,为使磁场右边界有粒子射出,加速电压至少应为多大?
(3)在有速度散射器的情况下,将加速电压调为U=U0,则穿过磁场的粒子中,穿越磁场的最短时间为多少?
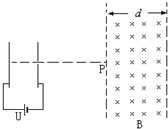
(1)在加速电场中根据动能定理:
qU0=
mv2 1 2
v=2qU0 m
在匀强磁场中,粒子做匀速圆周运动,洛伦兹力提供向心力,粒子刚好能从磁场的右边界穿过,轨迹正好是
个圆弧,即圆弧的半径为磁场的宽度d.则有:1 4
Bqv=mv2 d
d=mv Bq
解得:U0=B2qd2 2m
(2)此时的临界条件为:粒子沿磁场左边界射入磁场做半个圆的运动,从磁场右边界射出.
d=1 2 mv/ Bq
v/=2qU/ m
解得U/=B2qd2 8m
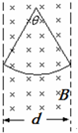
(3)做运动轨迹如右图所示.
U=U0=B2qd2 m
v=
=2qU m Bqd m
r=
=dmv Bq
从右图中得:最短时间的圆弧对的圆心角为θ=600
所以tmin=
T=1 6 πm 3Bq
答:(1)加速电场的电压为U0时,粒子刚好能从磁场的右边界穿过,则U0=
.B2qd2 2m
(2)若在P点加一个速度散射器(可使粒子速度方向变化,而不改变速度大小),使粒子从P点沿各个方向射入磁场,为使磁场右边界有粒子射出,加速电压至少应为
.B2qd2 8m
(3)在有速度散射器的情况下,将加速电压调为U=U0,则穿过磁场的粒子中,穿越磁场的最短时间为
.πm 3Bq
