问题
问答题
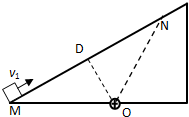
如图所示，粗糙程度均匀的绝缘斜面下方O点处有一正点电荷，D点为O点在斜面上的垂足，OM=ON．带负电的小物体以初速度v1=5m/s从M点沿斜面上滑，到达N点时速度恰好为零，然后又滑回到M点时速度大小变为v2=3m/s．若小物体电荷量保持不变，可视为点电荷．
（1）带负电的小物体从M向N运动的过程中电势能如何变化？电场力共做多少功？
（2）N点离斜面底边的高度h为多少？
（3）若物体第一次到达D点时速度为v=4m/s，求物体第二次到达D点时的速度v′．
答案
（1）电场力先做正功再做负功，电势能先减少后增加，
由于M、N为等势点，所以带电体在两点间运动时电场力做功为0
（2）设物体从M到N时，克服摩擦力做的功为Wf．
当物体从M到N时，由动能定理有：0-
mv12=-mgh-Wf1 2
当物体从N到M时，由动能定理有：
mv22-0=mgh-Wf1 2
联立解得：h=
=0.85m．v12+v22 4g
（3）由对称性可知从M到D以及从N到D克服摩擦力做功相等都为
．Wf 2
M到D：
mv2-1 2
mv12=-mg1 2
-h 2
+W电Wf 2
N到D：
mv′2-0=mg1 2
-h 2
+W电Wf 2
把h代入可得：
mv′2-1 2
mv2+1 2
mv12=1 2
m(v12+v22)1 4
v′=
=2v2-
(v12-v22)1 2
m/s．2
答：（1）电势能先减少后增加，电场力共做功0J．
（2）N点离斜面底边的高度h为0.85m．
（3）物体第二次到达D点时的速度为2
m/s．2