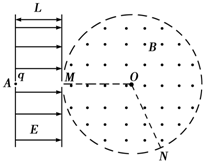
如图所示,空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场,电场强度为E、场区宽度为L.在紧靠电场右侧的圆形区域内,分布着垂直于纸面向外的匀强磁场,磁感应强度B未知,圆形磁场区域半径为r.一质量为m、电荷量为q的带正电的粒子从A点由静止释放后,在M点离开电场,并沿半径方向射入磁场区域,然后从N点射出,O为圆心,∠MON=120°,粒子重力可忽略不计.求:
(1)粒子经电场加速后,进入磁场时速度的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)粒子从A点出发到N点离开磁场经历的时间.
(1)设粒子经电场加速后的速度为v,根据动能定理有
qEL=
mv21 2
解得:v=2qEL m
(2)粒子在磁场中完成了如图所示的部分圆运动,设其半径为R,因洛仑兹力提供向心力,
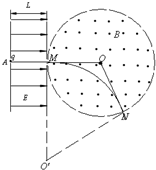
所以有qvB=mv2 R
由几何关系得
=tan30°r R
所以B=2mEL 3qr2
(3)设粒子在电场中加速的时间为t1,在磁场中偏转的时间为t2
粒子在电场中运动的时间t1=
=2L a 2mL qE
粒子在磁场中做匀速圆周运动,其周期为T=
=2πR v 2πm qB
由于∠MON=120°,所以∠MO'N=60°
故粒子在磁场中运动时间 t2=
T=60° 360°
T=1 6 πm 3qB
所以粒子从A点出发到N点离开磁场经历的时间t=t1+t2=
+2mL qE
=πm 3qB
+2mL qE
.πmr 6mqEL
答:(1)粒子经电场加速后,进入磁场时速度的大小为
;2qEL m
(2)匀强磁场的磁感应强度B的大小为
;2mEL 3qr2
(3)粒子从A点出发到N点离开磁场经历的时间为
+2mL qE
.πmr 6mqEL
