问题
问答题
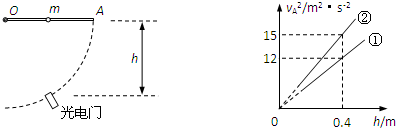
如图所示，长直均匀光滑杆一端固定在光滑转轴O处，在水平杆的另一端A下摆经过的轨迹上安装光电门，用来测量A端的瞬时速度vA．光电门测量位置和转轴O的高度差记为h．有一质量m=1kg的小球套在光滑杆上．
（1）若杆的质量忽略不计．小球固定在杆的中点处，静止释放．请写出光电门测量到的速度vA与高度差h的关系式．
（2）若杆的质量忽略不计．小球没有固定在杆上，仅套在杆的中点处．杆由静止释放后小球做自由落体运动，下落h后脱离杆，则小球脱离瞬间杆A端速度多大？
（3）实际情况下杆的质量M不能忽略，拿走小球后重复实验，得到了如图所示的vA2与h关系图线①．证明杆绕O点转动的动能Ek=
MvA2．1 6
（4）将小球固定在杆的中点后，得到vA2与h关系图线②．由①②两线，（g=10m/s2）求杆的质量M．
答案
（1）由机械能守恒定律得mg
=h 2
m(1 2
)2vA 2
解得vA=2gh
（2）由机械能守恒定律得mgh=
mv21 2
解得脱离时，小球速度v=2gh
因为小球从中点处释放，脱离时杆与水平方向夹角60°
由速度分解得vA=2gh 2
（3）由动能定理
Mg
=EKh 2
由图象得h=
vA21 30
得EK=
M1 6 v 2A
（4）由动能定理
mg
+Mgh 2
=h 2
m(1 2
)2+vA 2
M1 6 v 2A
得M=0.25kg
答：（1）光电门测量到的速度vA与高度差h的关系式为2
；gh
（2）小球脱离瞬间杆A端速度为
；2gh 2
（3）杆绕O点转动的动能EK=
M1 6
；v 2A
（4）杆的质量M为0.25kg．
还原为晶莹透明的晶体N，其结构中原子的排列为正四面体，请写出N及其2种同素异形体的名称____、______、_______。