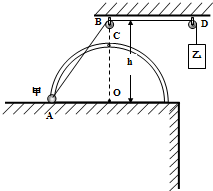
一个半径R为0.6m的光滑半圆细环竖直放置并固定在水平桌面上,O为圆心,A为半圆环左边最低点,C为半圆环最高点.环上套有一个质量为1kg的小球甲,甲可以沿着细环轨道在竖直平面内做圆周运动.在水平桌面上方固定了B、D两个定滑轮,定滑轮的大小不计,与半圆环在同一竖直平面内,它们距离桌面的高度均为h=0.8米,滑轮B恰好在O点的正上方.现通过两个定滑轮用一根不可以伸长的细线将小球甲与一个质量为2kg的物体乙连在一起.一开始,用手托住物体乙,使小球甲处于A点,细线伸直,当乙由静止释放后.
(1)甲运动到C点时的速度大小是多少?
(2)甲、乙速度相等时,它们的速度大小是多少?
(1)根据几何关系得:LAB=
=h2+R2
m=1m0.82+0.62
甲运动到C点时,甲的速度方向水平向右,所以乙的速度为零,对系统运用动能定理得:m乙g(LAB-LBC)-m甲gR=
m甲v甲21 2
解得:v甲=
m/s=4.47m/s. 2(2×10(1-0.2)-1×10×0.6) 1
(2)当连接甲球的细线与圆环相切时,甲、乙速度相等,此时甲球到达A'点,离开桌面的距离为d
根据几何关系得:LBA′=
=h2-R2
m=0.53m0.82-0.62
d=
=R2 h
m=0.45m0.62 0.8
对系统运用动能定理得:m乙g(LAB-LBA′)-m甲gd=
(m甲+m乙)v甲21 2
解得:v甲=2(m乙g(LAB-LBA′)-m甲gd) m甲+m乙
代入数据得:v甲=1.81m/s
答:(1)甲运动到C点时的速度大小是4.47m/s.
(2)甲、乙速度相等时,它们的速度大小是1.81m/s.
