如图(1)所示是根据某平抛运动轨迹制成的内壁光滑的圆管轨道,轨道上端与水平面相切.实验得到进入圆管上端时的水平速度v0的平方和离开圆管时速度的水平分量vx的平方的关系如图(2)所示.一质量为m=0.4kg、体积很小的滑块静止在距离管口L=1m处,滑块与水平面间的动擦因数为μ=0.2.(g=10m/s2)
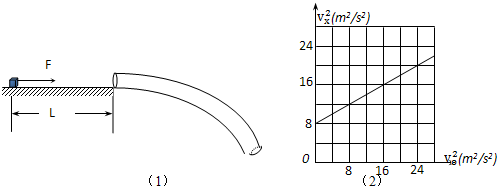
(1)当滑块以水平速度v0=8m/s从轨道进入后,离开轨道时的水平速度是多大?
(2)用大小为F=5N的水平恒力在水平面上拉动滑块一段距离x后撤去F,要使滑块进入圆管轨道后在轨道内运动过程中水平分速度不断增大,求x的取值范围.
(3)当滑块以水平速度v0=3m/s从轨道顶端进入后,当其到达轨道底部时的速度大小是多少?
(1)由图象(2)得
=8+v 2x 1 2 v 20
当v0=8m/s时,vx=
=28+
×821 2
m/s10
(2)根据动能定理得
Fx-μmgL=
mv21 2
由图象(2)知,要使滑块进入圆管轨道后在轨道内运动过程中水平分速度不断增大,应满足0<v<4m/s,
联立解得:x的取值范围为0.16m<x<0.8m
(3)滑块在管道中运动过程机械能守恒,则有
mv2=mgh+1 2
m1 2 v 20
得 v2=2gh+v 20
(nvx)2=2gh+v 20
解得,vx=
+2gh n2 v 20 n2
由图象可得
=1 n2
,1 2
=82gh n2
则得v2=8+v 20
得 v=
=16+ v 20
=5m/s16+9
答:(1)当滑块以水平速度v0=8m/s从轨道进入后,离开轨道时的水平速度是2
m/s.10
(2)x的取值范围为0.16m<x<0.8m.
(3)滑块到达轨道底部时的速度大小是5m/s.
