已知函数f(x)=loga
(1)求f(x)的定义域; (2)判断f(x)的奇偶性; (3)讨论f(x)的单调性,并证明. |
(1)因为
>0,解之得x<-b或x>b,x+b x-b
∴函数的定义域为(-∞,-b)∪(b,+∞).…(3分)
(2)由(1)得f(x)的定义域是关于原点对称的区间
f(-x)=loga
=loga-x+b -x-b
,x-b x+b
∵-f(x)=loga(
)-1=logax+b x-b
,x-b x+b
∴f(-x)=-f(x),可得f(x)为奇函数.…(6分)
(3)证明:设b<x1<x2,则
f(x1)-f(x2)=loga
,(x1+b)(x2-b) (x2+b)(x1-b)
∵
-1=(x1+b)(x2-b) (x2+b)(x1-b)
>02b(x2-x1) (x2+b)(x1-b)
∴当a>1时,f(x1)-f(x2)>0,可得f(x1)>f(x2),f(x)在(b,+∞)上为减函数;
当0<a<1时,f(x1)-f(x2)<0,可得f(x1)<f(x2),f(x)在(b,+∞)上为增函数.
同理可得:当a>1时,f(x)在(-∞,-b)上为减函数;当0<a<1时,f(x)在(-∞,-b)上为增函数.
综上所述,当a>1时,f(x)在(-∞,-b)和(b,+∞)上为减函数;当0<a<1时,f(x)在(-∞,-b)和(b,+∞)上为增函数.…(12分)

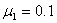 ,在木板的左端放置一个质量为m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数
,在木板的左端放置一个质量为m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数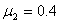 ,取g=10m/s2,试求:
,取g=10m/s2,试求:
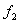 随拉力F大小变化的图像。(设木板足够长)
随拉力F大小变化的图像。(设木板足够长)