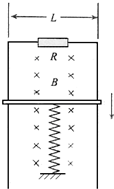
如图所示,固定的竖直光滑金属导轨间距为L,上端接有阻值为R的电阻,处在方向水平、垂直导轨平面向里的磁感应强度为B的匀强磁场中,质量为m的导体棒与下端固定的竖直轻质弹簧相连且始终保持与导轨接触良好,导轨与导体棒的电阻均可忽略,弹簧的劲度系数为k.初始时刻,弹簧恰好处于自然长度,使导体棒以初动能Ek沿导轨竖直向下运动,且导体棒在往复运动过程中,始终与导轨垂直.
(1)求初始时刻导体棒所受安培力的大小F;
(2)导体棒往复运动一段时间后,最终将静止.设静止时弹簧的弹性势能为Ep,则从初始时刻到最终导体棒静止的过程中,电阻R上产生的焦耳热Q为多少?
(1)设导体棒的初速度为v0,由动能的定义式
Ek=
m1 2
得 v0=v 20 2Ek m
设初始时刻产生的感应电动势为E,由法拉第电磁感应定律得:
E=BLv
设初始时刻回路中产生的电流为I,由闭合电路的欧姆定律得:
I=E R
设初始时刻导体棒受到的安培力为F,由安培力公式得:F=BIL
联立上式得,F=B2L2 R 2Ek m
(2)从初始时刻到最终导体棒静止的过程中,导体棒减少的机械能一部分转化为弹簧的弹性势能,另一部分通过克服安培力做功转化为电路中的电能,因在电路中只有电阻,电能最终全部转化为电阻上产生的焦耳热Q.
当导体棒静止时,棒受力平衡,此时导体棒的位置比初始时刻降低了h,
则 mg=kh,得h=mg k
由能的转化和守恒定律得:mgh+Ek=EP+Q
解得 Q=
+Ek-Epm2g2 k
答:
(1)初始时刻导体棒所受安培力的大小F为B2L2 R
;2Ek m
(2)从初始时刻到最终导体棒静止的过程中,电阻R上产生的焦耳热Q为
+Ek-Ep.m2g2 k
