问题
问答题
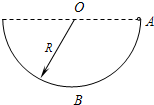
如图所示,光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低位置B时,球对轨道的压力为2mg.求:
(1)小球受到电场力的大小和方向;
(2)带电小球在滑动过程中的最大速度.
答案
(1)设小球运动到最底位置B时速度为v,此时N-mg=
…①mv2 R
解得:v=gR
若不受电场力,则
mgR=
mv′21 2
解得:v′=2gR
因为v′>v
所以此过程中电场力做负功,电场力方向水平向右
设电场力大小为F,由题意,小球从A处沿槽滑到最底位置B的过程中,根据动能定理得:
mgR-FR=
mv2-0…②1 2
由①、②两式得:F=
mg…③,方向水平向右1 2
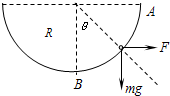
(2)小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,如图
mgsinθ=Fcosθ…④
由④得:tanθ=1 2
小球由A处到最大速度位置得过程中mgR-cosθ-
mgR(1-sinθ)=1 2
m1 2
-0v 2m
得:vm=Rg(
-1)5
答:(1)小球受到电场力的大小为
mg,方向水平向右;1 2
(2)带电小球在滑动过程中的最大速度.
